發布時間:2019-11-14 瀏覽量:1950
0 引言
隨著供暖熱計量的發展,供暖系統的水力運行工況將由靜態變換為動態。這種工況的變化,使得在系統上探討調節問題已無意義,因為一種固定的管路結構模式只能適應特定的水力工況,動態工況只能靠局部調節裝置加以控制[1]。
對動態水系統而言,通常設置的調節裝置種類很多,例如流量調節閥、壓差限制器等,這些設備的控制對象是流量,包括流量變化及流量穩定,而采取的技術手段則是改變局部管路的流動阻力。由于局部管路流動阻力的變化,使得相鄰并聯環路必然受到影響。為實現相鄰環路之間互不影響,筆者提出三通調節閥的定流量調節形式。
1 調節形式
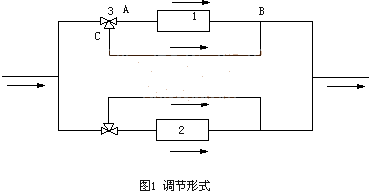
如圖1所示,1,2為兩并聯環路(用戶),為散熱器或風機盤管;3是三通調節閥;AB為1所在支路,CB為一旁通支路。當用戶1要求流量變化時,調節三通調節閥3,使得AB支路流量增大或減小,與此同時,CB支路流量將減小或增大,但在任意調節條件下滿足式(1):
GAB+GCB=G0 (1)
式中:GAB為AB支路流量;
GCB為CB支路流量;
G0為兩支路的流量總和。無論GAB,GCB如何變化,G0不變。
式(1)就是該調節形式所應具備的調節特性稱其為定流量特性。由于G0保持不變,無論三通調節閥如何調節,都不會影響環路2或其他相鄰環路。
2 調節阻力特性
在并聯環路中既然改變某支路流量并不影響相鄰支路,那么調節特性就與其他支路無關。對于某一確定支路,其阻力特性是固定不變的,而對于某一已知閥門其阻力特點及其調節特性也是確定的,因此要實現閥門安裝在該支路上后調節具有定流量特性,有三種可能[2]:
a)此三通調節閥與該支路完全匹配,調節是定流量;
b)在該支路上增加局部阻力,使其阻力特性變化后與閥匹配;
c)改造閥門結構,使其阻力特性或調節特性發生變化后與支路匹配。
三種可能說明調節特性并不是某一特性所能決定的,而是相互關聯的,因此分析其綜合阻力關聯式是必要的。
閥門的調節特性一般用特征曲線來描述,特征曲線是由相對開度K與相對流量GK的關系決定的,可表示為(定壓差條件下):
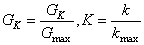 (2)
(2)
式中:Gk為閥門某一開度所通過的流量,
Gmax為所通過的最大流量;
k為任意開度,kmax為最大開度。
將流動阻力特性引入,有:
Δp=SkGk2 (3)
式中 Δp為閥兩端壓差,調節時為定值;Sk為任意開度下阻力特性系數。
將式(2)代入式(3)中,有:
Δp=SkGk2max2 (4)
又
Δp=Skmax Gmax2 (5)
將式(4)與式(5)相比,得
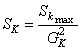 (6)
(6)
三通調節閥有直通與旁通支路,兩路開度相反,由式(6)得到:
直通支路閥的阻力特性Sk計算式為:
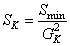 (7)
(7)
旁通支路閥的阻力特性Skmax-k計算式為:
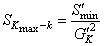 (8)
(8)
式中:Smin為直通全開阻力特性系數,
S'min為旁通全開阻力特性系數;
G'K為旁通支路閥的相對流量。
考慮支路的阻力特性以后,則調節時綜合阻力特性式如下:
直通支路的阻力特性式:
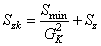 (9)
(9)
旁通支路的阻力特性式:
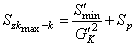 (10)
(10)
由式(1)得直通支路與旁通支路的并聯阻力特性式為:
Szk-0.5+Szkmax-k-0.5=Sb-0.5 (11)
式中:Sb為并聯特性系數,下角z代表綜合阻力特性參數。當直通全開或旁通全開時,Sb=Smin+Sz或Sb=S'min+Sp,Sp為旁通特性系數。
因此定流量調節所滿足的阻力特性條件可由下面的方程組[3]描述:
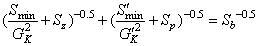 (12)
(12)
Sb=Smin+Sz,Sb=Smin+Sp (13)
式(12)與(13)即為總阻力關聯式。
3 三通調節閥阻力性能測試
3.1 測試及測試原理
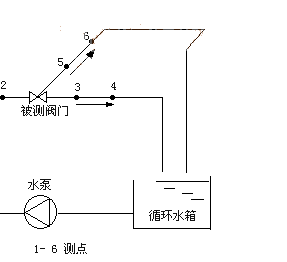
閥門阻力特性測試如圖2所示。水自循環水箱被水泵抽取,經測壓點1,2,被測閥門及測壓點3,4,或經測點1,2,被測閥門及測壓點5,6流回循環水箱。
壓強采用測壓管直接測得,流量采用體積法測量。
閥門阻力系數計算公式為:
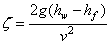 (14)
(14)
式中:ζ為閥門局部阻力系數;
hw為閥門前后測點間總水頭損失,m,hw=h2- h4或hw=h2- h6;
hf為相應測點間沿程水頭損失,m,hf=l24/l12(h1- h2)或hf= l26/l12(h1- h2),其中h1~h6分別為對應點的測壓管水頭,l24為測點2,4間管長,m,l12為測點1,2間管長,m,l26為測點2,6間管長,m;
v 為測試段管內斷面平均流速,m/s,v= 4Q/πd2,其中Q為流量,m3/s,d為管徑,m。
3.2 測試結果
a)直通全開工作狀態阻力系數ζmin=4.60;
b)旁通全開工作狀態阻力系數ζ'min=8.47;
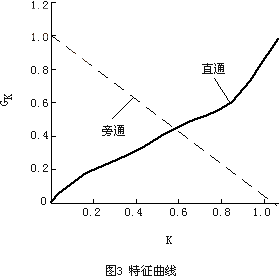
c)閥門相對開度與相對流量關系曲線見圖3。
4 應用分析
為保證供暖系統各并聯環路動態調節時互不影響,設計了如圖1所示調節形式,具體形式見圖4。
圖中1,2為散熱器,3為三通調節閥,A-1-B為直通支路,CB為旁通支路,支路還存在一些彎頭。
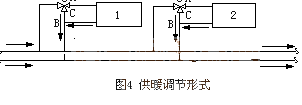
常用的三通調節閥有3種,按直通配管管徑可分為:DN15,DN20,DN25。由于散熱器的局部阻力實際可取為定值,為便于應用與推廣,將其結構模塊化,統一設計為DN25。另外,為計算方便,將管路的沿程阻力轉化為局部阻力,稱之為當量局部阻力。由此,支路的總阻力為當量局部阻力與局部阻力之和[3~4]:
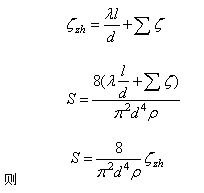 (15)
(15)
式中:λ為摩擦阻力系數。
支路(全開)的局部阻力系數[4]見表1。
直通支路全開或旁通支路全開的總局部阻力系數相差不到1%,其流量也在此范圍之內。然而當閥門在其他開啟度條件下并不一定也是如此。由式(9),(10),(15),可得到直通或旁通支路總局部阻力系數:
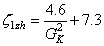 (16)
(16)
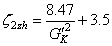 (17)
(17)
式中 ζ1zh為直通支路總局部阻力系數,ζ2zh為旁通支路總局部阻力系數。
由式(16),(17)及圖3,插值計算得到表1所示結果。
表1 不同開度條件下的阻力系數
K | |||||||
1 | 0.8 | 0.6 | 0.5 | 0.4 | 0.2 | 0 | |
ζ1zh | 11.9 | 16.7 | 21 | 30 | 32.2 | 122.3 | ∞ |
ζ2zh | ∞ | 139.1 | 52.9 | 45.3 | 28 | 16.8 | 12 |
ζzh | 11.9 | 9.2 | 8 | 9.1 | 7.5 | 8.9 | 12 |
當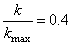 時,并聯總阻力系數為7.5,與全開或全閉的12相比,變化了38%,在定壓條件下,流量要變化27%。若不定壓,屬自然調節,流量變化會減小到20%左右,這由管網的自適應能力決定。
時,并聯總阻力系數為7.5,與全開或全閉的12相比,變化了38%,在定壓條件下,流量要變化27%。若不定壓,屬自然調節,流量變化會減小到20%左右,這由管網的自適應能力決定。
5 定流量特征曲線
特征曲線包括直通曲線與旁通曲線,要實現定流量,兩條曲線可能有多種組合,但這兩條曲線組合并非是任意的,第一,要符合實際,即在制造工藝上是否可行;第二,要利于將來的調節。為有利于動態調節,將直通曲線設為線性的,旁通曲線由直通的線性決定。即直通曲線為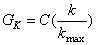 是一條已知曲線,C是一待定常數,求旁通曲線GK。
是一條已知曲線,C是一待定常數,求旁通曲線GK。
以上述的應用為例,兩曲線應滿足的關系式為:
ζ1zh-0.5+ζ2zh-0.5=ζzh-0.5
將式(16),(17)代入得:
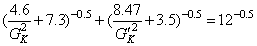 (18)
(18)
由上式經插值計算后再進行曲線擬合,G'K為一指數或對數曲線,見圖5。
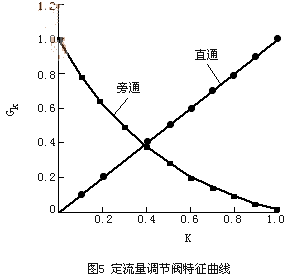
在常用的閥門中,其特征曲線通常為線性(不絕對)或對數曲線,一個閥門具有這兩種特征曲線,可以看作是一個線性調節閥與一個對數調節閥的組合,因此,生產具有線性與對數混合調節特征的閥門在工藝上是可行的。
6 結論
6.1 三通調節閥的調節形式較其他調節方式有明顯優點,調節時阻力不變、流量恒定,能實現并聯環路之間動態調節互不影響。
6.2 要達到定流量目的,阻力分配必須滿足一定關系,由于結構模塊化,實際支路的阻力特性將由閥門結構決定,閥的兩特征曲線組合是該調節形式成功應用的關鍵。
6.3 實驗測試的調節閥特征曲線為兩不絕對的線性曲線,應用該閥時,最大流量偏差為27%,當管網達到一定的穩定性時,流量偏差在20%左右。
6.4 定流量調節閥的特征曲線為線性曲線與對數曲線組合,或指數曲線與對數曲線組合。不同的曲線組合時,流量誤差在10%以內,即認為具有可用性。
參考文獻
[1] 石兆玉,編著.供暖系統的運行調節與控制.北京:清華大學出版社,1994
[2] 江億.管網可調性和穩定性的定量分析.暖通空調,1997,27(3)
[3] 張維佳,潘達林,編著.工程流體力學.北京:中國建筑工業出版社,2001
[4] 賀平,孫剛,編著.供熱工程.北京:中國建筑工業出版社,1996
本文鏈接:http://szruifeng.com/news/detail/20191114100431.html
版權所有:調節閥廠家-杭州杜伯拉閥門科技有限公司 浙ICP備18052799號-4